Actividad 1
Clasifica cada elemento según corresponda: materia del argumento, contenido del argumento o
forma del argumento.
Si p entonces q
No q
∴ No p
Proposiciones
Conceptos
Animales
Fotografía
Si p entonces q
p
∴ q
Educación
p o q
No p
∴ q
Contaminación
Si p entonces q
Si q entonces r
∴ si p entonces r
Limpiar
Revisar
Revisa tus respuestas, algunas no son correctas.
¡Bien hecho!
pasa a la siguiente actividad.
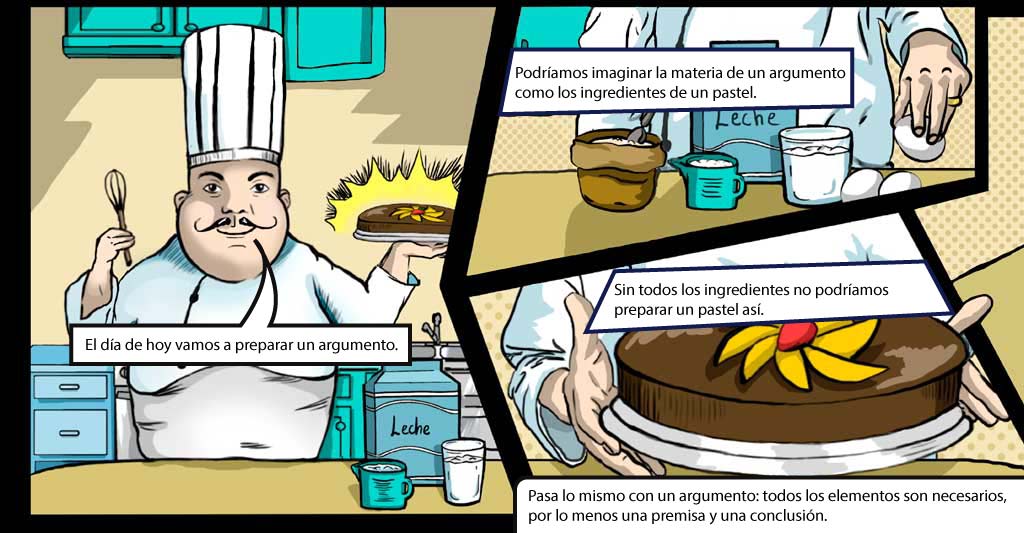
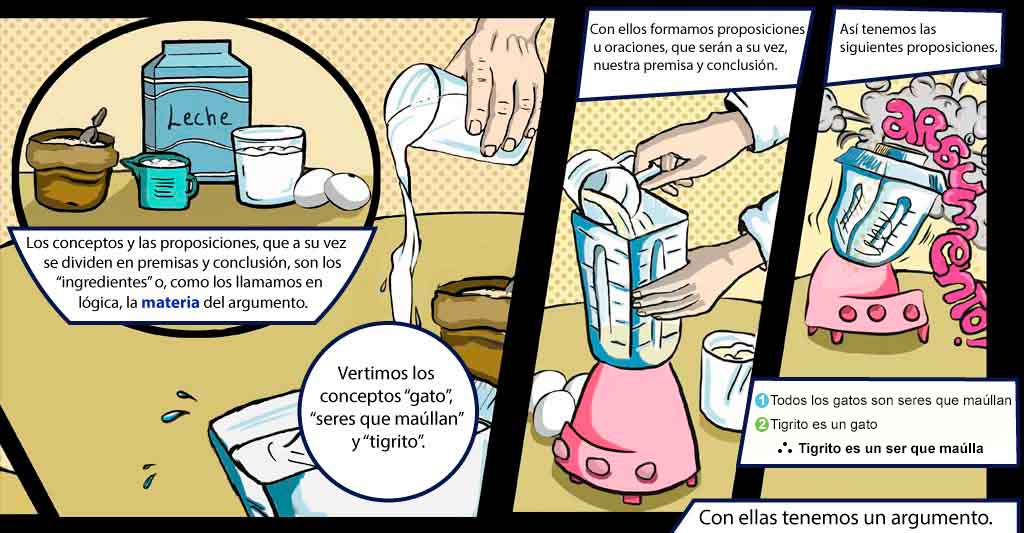
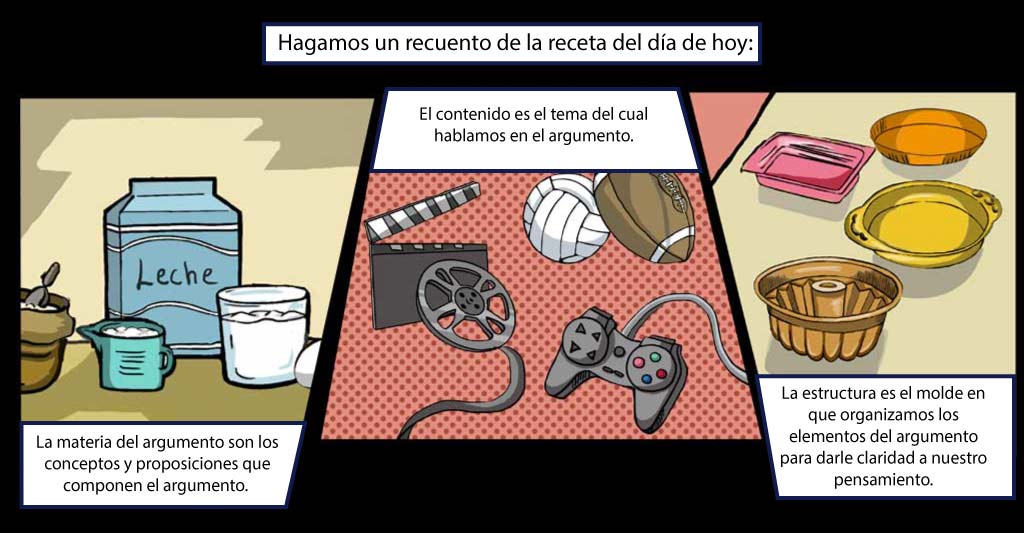
La materia de un argumento consiste en los conceptos y las
proposiciones que se elaboran sobre un tema determinado.
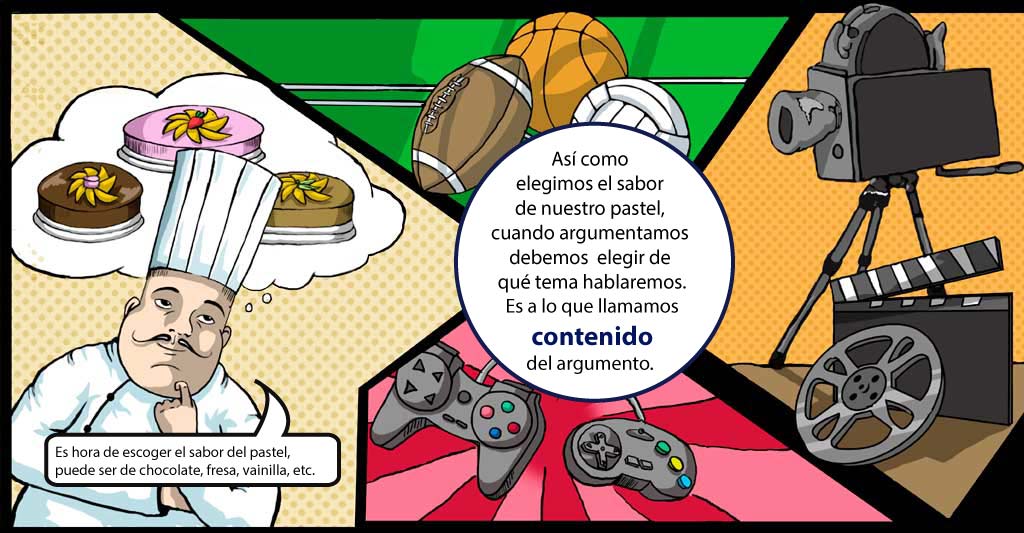
El contenido es el tema del que trata el argumento.
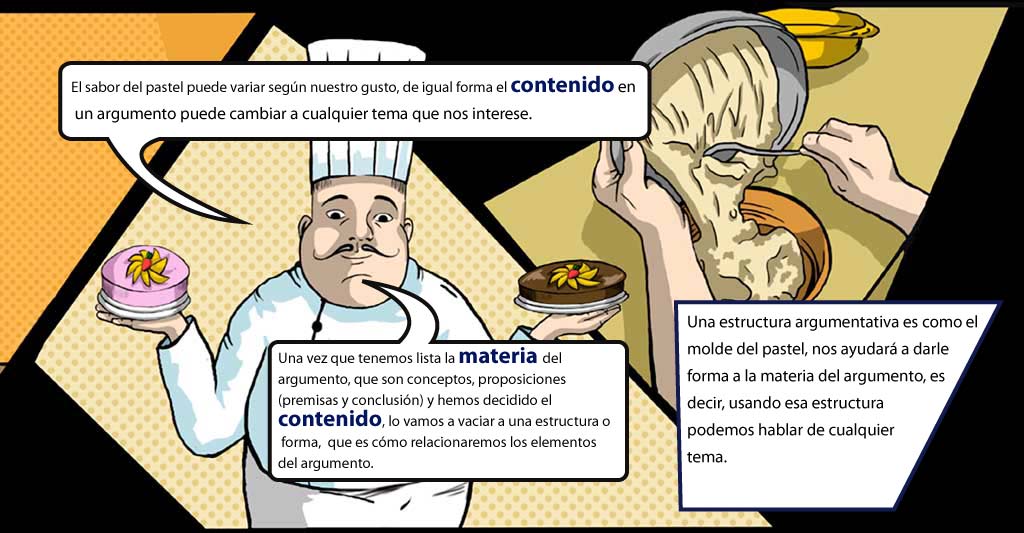
La estructura sirve para organizar los elementos del argumento.
Conclusiones
Como ya vimos, un argumento está compuesto de:
Contenido:
Tema del que trata el argumento
Materia:
Son los conceptos y proposiciones
(que a su vez se dividen en premisas y la conclusión)
Estructura argumentativa:
Nos guía en cómo organizamos los elementos de nuestro argumento.
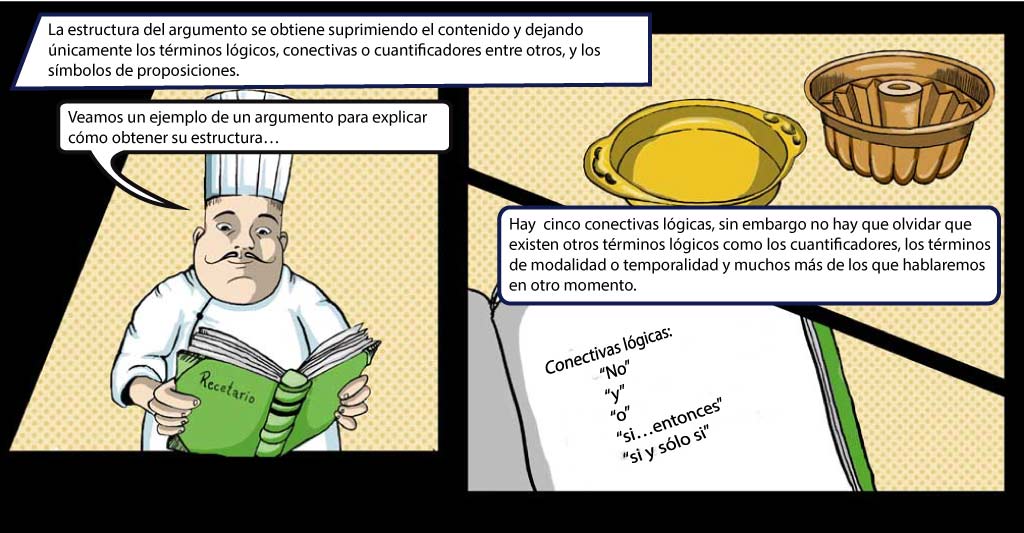
Se obtiene la estructura de un argumento si se suprime el contenido y dejamos solo las
conectivas lógicas y los símbolos de las proposiciones.
Lo anterior nos permite entender, utilizar e identificar las estructuras que se usan en la lógica.
Si p entonces q
No q
∴ No p
Si p entonces q
Si q entonces r
∴ Si p entonces r
Argumento
Si yo corro diario 30 minutos, entonces seré una persona saludable.
Yo corro diario 30 minutos.
Por lo tanto, yo seré una persona saludable.
{
Materia:
Son los conceptos y proposiciones que componen el argumento.
Ejemplo:
p = Yo corro diario 30 minutos.
q = Yo seré una persona saludable.
Contenido:
Es el tema del cual se habla en el argumento.
Ejemplo:
Salud
Estructura:
Es la manera en que se organizan los elementos del argumento.
Ejemplo:
Si p entonces q
p
∴ q
Para obtener la estructura de un argumento:
1.- Identifica las conectivas lógicas del argumento.
2.- Determina cuántos enunciados hay en el argumento,
éstos los puedes identificar fácilmente si haces explícito el sujeto.
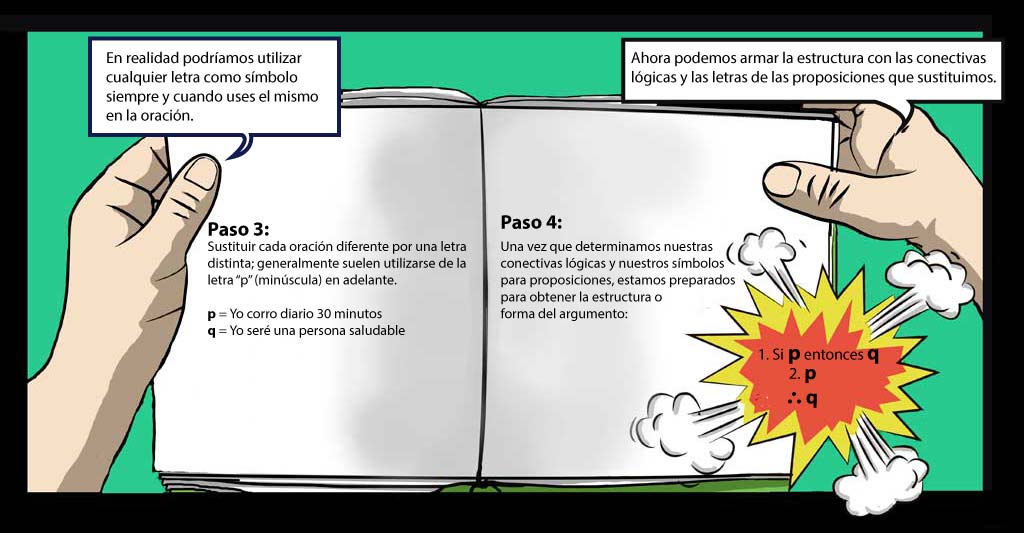
3.- Sustituye los enunciados por letras en minúsculas, generalmente se suele utilizar de la "p" en adelante.
4.- Obtén la estructura del argumento utilizando las conectivas lógicas y los símbolos para las proposiones.
Si yo corro diario 30 minutos entonces seré una persona saludable
Yo corro diario 30 minutos.
∴ Yo seré una persona saludable.
p = Yo corro diario 30 minutos.
q = Yo seré una persona saludable.
Si p entonces q
p
∴ q
X